Redes neuronales artificiales
A juicio de Rumelhart, el cognitivismo clásico centró sus esfuerzos explicativos de la mente en el nivel lógico o funcional, es decir, se consideraba a la mente como un programa de ordenador (software) y se suponía que dicho programa podría ejecutarse en cualquier máquina, pues se entiende que el nivel físico, es decir, el cerebro (wetware), se basará en sistemas de propósito general de tipo von Newmann. Esto se conoce como la metáfora del ordenador.
Los conexionistas, sin embargo, dirigieron su mirada al nivel de implementación, el cerebro, pues consideraban que a partir de él se podrían diseñar más adecuadamente algoritmos que se puedan utilizar para explicar los fenómenos mentales. Por lo tanto, la metáfora del ordenador fue sustituida por la metáfora cerebral de la mente abandonando la computación de estilo simbólico por una computación inspirada en el funcionamiento cerebral.
Al mirar hacia la mente, lo primero que se observó, gracias a los pioneros trabajos de Santiago Ramón y Cajal fue un entramado de células conectadas entre sí. Estas células, las neuronas se pueden dividir funcional y anatómicamente en tres zonas: el cuerpo celular o soma, axón y dendritas. Cada neurona recibe información a través de las dendritas, la procesa principalmente en el soma y la proyectan a través del axón. La conexión entre axones y dendritas recibe el nombre de sinapsis. El siguiente video muestra un resumen de lo que son las neuronas.
En 1943, dos neurocientíficos, Warren McCulloch y Walter Pitts, propusieron un modelo de neurona básico siendo pioneros en el intento de definir formalmente las neuronas como elementos computacionales y en explorar las consecuencias de sus propiedades. Desde su definición, a pesar de los grandes avances en el campo de la neurociencia, las redes neuronales artificiales no han cambiado mucho con respecto a las que propusieron en su día McCulloch y Pitts.
Es importante recalcar que dicho modelo no pretende ser una teoría del funcionamiento del cerebro del cual cada día se descubren cosas nuevas sino más bien la definición de un modelo de computación inspirado en el cerebro que permita diseñar sistemas artificiales inteligentes para resolver problemas concretos.
Diseccionando la neurona artificial
Al igual que sus homologas biológicas, cada neurona consta de varias entradas y de una salida. Una neurona recibe información del entorno o de otras neuronas a través de las conexiones o sinapsis de sus entradas. La información recibida determinará el estado o nivel de activación de la neurona en base a una función de activación.
El estado de una neurona puede tomar valores continuos o discretos. Las neuronas descritas por McCulloch y Pitts podían estar únicamente en dos estados: activadas (1) y desactivadas (0). El estado de una neurona se transmitirá a su salida a través de la función de salida, que típicamente será la función identidad, es decir, el estado será igual a la salida.
Formando redes neuronales
De forma análoga a como las neuronas del cerebro crean complejos circuitos, una red neuronal artificial está formada por múltiples neuronas conectadas entre sí.
Las conexiones entre las neuronas se definen utilizando un parámetro denominado peso sináptico. Dependiendo de si el peso es positivo o negativo la naturaleza de la conexión será excitante o inhibitoria. Además, el valor absoluto del peso indicará la fuerza de la conexión.
Si tenemos una neurona activada cuya salida este conectada a varias neuronas, esta neurona propiciara la activación de las neuronas con las cuales se conecta a través de conexiones excitantes y dificultara la activación de aquellas neuronas con las cuales se conecte a través de conexiones inhibitorias. Todo ello con una fuerza proporcional al valor absoluto del peso de la conexión.
El valor de todos los pesos de la red neuronal en un momento temporal dado es lo que va a especificar el patrón de conectividad que será lo que determine como responderá la red a las señales que reciba. Los procesos de aprendizaje de las redes neuronales se basan en ir ajustando el patrón de conectividad hasta que la red se comporte de la forma deseada para un problema concreto. Existe diversas técnicas para ello. Algunas redes neuronales se ‘entrenarán’ para un problema concreto y posteriormente se impedirá el reajuste de su patrón de conectividad durante su funcionamiento mientras que otras técnicas de aprendizaje pueden permitir a la red adaptarse modificando su patrón de conectividad sobre la marcha.
Ejemplo
En el siguiente diagrama se muestran las conexiones de una red neuronal (ANN) formada por 9 neuronas: {a, b, c, d, e, f, g, h, i}. Además, en cada conexión se muestra su peso sináptico, que se recuerda que indica la naturaleza y la fuerza de esa conexión.
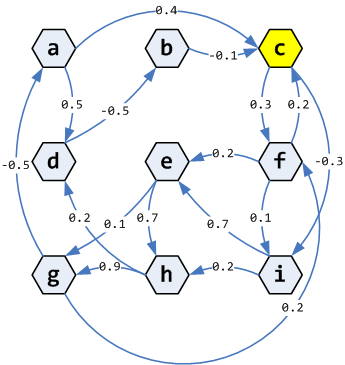
De forma alternativa, el diagrama anterior puede verse como una matriz de nxn, siendo n el número de neuronas, que representa el patrón de conectividad. Además, podemos representar el estado o nivel de activación de cada neurona como un vector columna de tamaño n. En la figura siguiente podemos ver tanto la matriz de conexiones como el vector de estado de las neuronas.
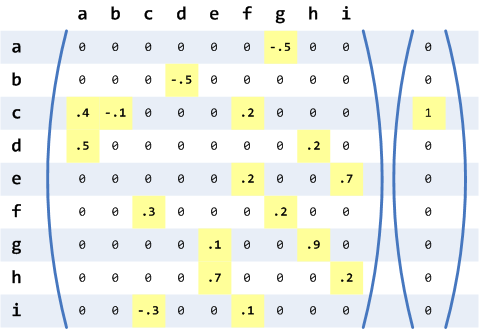
Las columnas indican el origen de las conexiones y las filas el destino. Así si miramos a la primera columna y la tercera fila tenemos que la neurona ‘a’ está conectada a la neurona ‘b’ con una fuerza de ‘0.4’ tal y como se podía ver en el grafo. Además, si observamos el vector de estado vemos que inicialmente la única neurona activa es la ‘c’ (recordemos que en el modelo que estamos considerando una neurona solo puede estar activada o desactivada).
La función de activación utilizada es la función escalón. Para cada neurona, se calculará el sumatorio de todos los niveles que ingresa procedentes de otras unidades. Dicho sumatorio se conocerá como el valor que ingresa la neurona y será suministrado a la función de activación. En el caso de la función escalón, la salida será 1 (activación) en el caso de que su ingreso sea mayor que cero y 0 (inhibición) en caso contrario.
La vista matricial de la figura anterior facilita calcular los ingresos de la función de activación de cada neurona ya que lo reduce a una simple multiplicación matricial. Podemos simular la red neuronal multiplicando la matriz de conexiones por el vector de estado de tal forma que obtengamos un nuevo vector de estado.
Si calculamos los ingresos a partir de la figura anterior, es decir, realizamos la multiplicación, obtendremos el vector [0 0 0 0 0 0.3 0 0 –0.3] y al aplicar la función de activación a cada uno de sus valores tendremos [0 0 0 0 0 1 0 0 0]. Es decir, la red ha pasado de tener la neurona ‘c’ activa a tener la neurona ‘f’ activa en una iteración o instante temporal. La aplicación recurrente de este procedimiento nos permite calcular la evolución de la red que en el caso que nos ocupa se muestra en la siguiente figura.
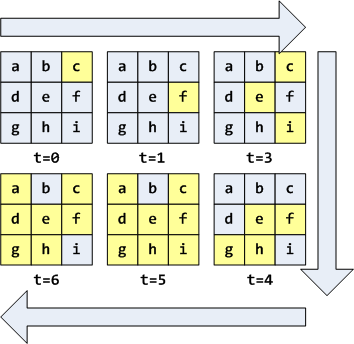
Algunas redes cambiaran indefinidamente a lo largo del tiempo, sin embargo, la red anterior, alcanzará el estado estacionario mostrado en t=6 para la mayoría de condiciones iniciales, lo cual convierte a dicho estado en un atractor puntual para esta red. El otro atractor de la red es el estado cero en el cual todas las neuronas estan desactivadas. Cualesquiera que sean las condiciones iniciales de esta red, a medida que evoluciona, terminará estancándose en uno de sus dos estados atractores.
La arquitectura de la red anterior es recurrente, y dispersa. Recurrente porque contiene bucles en las conexiones ( c->f->c ) y dispersa porque de todas las conexiones posibles (n^2=81), solo unas pocas se han realizado. Existen múltiples arquitecturas de redes neurales dependiendo de cómo se estructuran y conectan las neuronas que las componen.