Diamante - Cuadrado
Las extensiones de terreno son uno de los fenómenos naturales más comúnmente representados gráficamente por computador.
El algoritmo Diamond-Square (Diamante-Cuadrado) es un método utilizado para la generación de terreno de forma aleatoria. Fue desarrollado por Loren Carpenter, cofundador y científico jefe de Pixar, para ser usado en el modelado de una superficie planetaria.
Los resultados producidos por dicho método se pueden observar en el siguiente video, generado por un programa cuyo código fuente puede encontrar adjunto a este artículo.
Para modelar el terreno se comienza con una matriz de dimensiones mxn, donde típicamente m será igual a n ya que esto simplifica las cosas. Las dimensiones de la matriz deberán ser potencia de dos más 1, es decir, 33x33, 65x65, 129x129, 257x257, etc.
Los valores de la matriz se interpretan como la altura que tiene el terreno en ese punto, por lo que un valor en la posición 30,30 de 65 significa que en la posición 30,30 del terreno, su altura es de 65 unidades. Este tipo de matrices se conocen como ‘heightmap’ o mapa de alturas.
La siguiente figura, extraída de la publicación original, muestra el proceso de generación de las alturas para una matriz de 5x5.
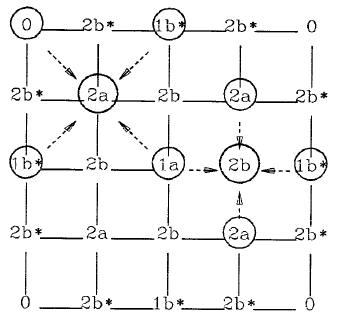
El proceso comienza con las cuatro esquinas, marcadas como 0, es decir, con un ‘cuadrado’ cuyos valores de altura son inicializados a los valores de altura que deseemos, en nuestro caso serán inicializados con el valor 0.
A continuación, se utilizan dichos valores para calcular la altura del punto 1a. Las etapas del algoritmo marcadas como a (1a, 2a, 3a, etc.) forman la parte ‘diamante’ del proceso, ya que si trazamos las diagonales desde cada punto a cada una de las esquinas del ‘cuadrado’ se formara un patrón de rombos, símbolo que habitualmente se utiliza para representar a los diamantes.
Después se procede a la etapa ‘cuadrado’ por lo que se toman las esquinas de cada uno de los rombos generados para calcular un nuevo valor para su centro, puntos marcados como 1b.
Una vez realizadas las etapas diamante y cuadrado podemos observar que la matriz o rejilla ha quedado dividida en 4 cuadrados.
El algoritmo continúa entonces con una nueva fase diamante-cuadrado, marcada como 2ª y 2b, solo que esta vez partiremos de 4 cuadrados en lugar de 1 y a cuya resolución la rejilla quedará dividida en 16 cuadrados.
En este caso el proceso ha concluido porque todos los puntos de la matriz han sido asignados. Si hubiéramos comenzado con una matriz de dimensiones mayores el proceso continuaría con nuevas etapas diamante-cuadrado hasta que quedase totalmente dividida y todos sus puntos hubiesen sido asignados con su correspondiente valor de altura.
Para calcular la altura de cada punto se utiliza el promedio de los valores circundantes, es decir, los cuadrados en la etapa diamante, y las esquinas de los rombos en la etapa cuadrado. A dicho valor, posteriormente se le añade un valor aleatorio (entre –d y +d) que estará limitado por unos parámetros.
Puede observar los detalles en la implementación adjunta a este artículo. Dicha implementación está basada en el programa de Paul Martz publicada en Generating Random Fractal Terrain y utiliza XNA para la representación grafica.